Introduction

Understanding evolutionary relationships is fundamental to biology, providing valuable insights across various disciplines, including comparative genomics, molecular evolution, developmental biology, adaptation, speciation, community assembly, and ecosystem functioning.

Phylogenetic analysis is the study of evolutionary relationships using computational methods, typically based on the comparison of DNA or protein sequences from different species. A key aspect of this analysis is the construction of a phylogenetic tree, a hierarchical structure that represents the evolutionary relationships between a set of taxa, which may include species or genes. Since phylogenetic trees can contain elements beyond just species, the entities at the tree’s leaves are generally referred to as taxa. Phylogenetic analysis is also one of the most computationally intensive areas of modern biology due to the complexity of sequence comparisons and tree reconstruction algorithms.

One of the primary methods for studying evolutionary relationships among biological species or genes is through the construction of phylogenetic trees or guide trees. Taxa that share a close evolutionary relationship are positioned closer together in the tree, whereas those that are more distantly related appear farther apart. Longer branches indicate greater evolutionary divergence, reflecting a higher degree of genetic change from a common ancestor. Branches that diverge closer to the root represent ancient evolutionary splits, while those that split further from the root indicate more recent divergence, meaning these taxa are more closely related.

A prerequisite for constructing a phylogenetic tree is a multiple sequence alignment (MSA) file, which aligns two or more biological sequences to identify regions of similarity and establish a consensus sequence. Various computational methods are used to construct phylogenetic trees, including distance-based, character-based, and probabilistic approaches, each offering unique advantages depending on the dataset and research question:

 

1. Distance based methods

Distance matrix-based methods calculate the genetic distance from multiple sequence alignments. This is one of the simplest methods that can be implemented. These methods do not invoke an evolutionary model.

a. Clustering algorithms

i. Unweighted Pair Group Method with Arithmetic Mean (UPGMA)

ii. Neigbor joining (NJ)

b. Optimality based algorithms

I. Fitch Margoliash

II. Minimum evolution method

 

2. Character based methods

These methods analyze individual sequence characters (nucleotides or amino acids) to infer evolutionary relationships. Unlike distance-based methods, they explicitly consider evolutionary models.

a. Maximum Parsimony

A simple method that assumes the most likely phylogenetic tree is the one that requires the fewest evolutionary changes. It represents an implicit model of evolution (parsimony principle).

b. Maximum likelihood

A statistically rigorous approach that estimates the tree with the highest likelihood given a specific evolutionary model.

c. Bayesian

Uses a Bayesian framework, which explicitly incorporates an evolutionary model and prior probabilities to estimate phylogenetic relationships.

 

Neighbor joining algorithm

The Neighbor-Joining (NJ) algorithm is a distance-based method used to construct both phylogenetic (evolutionary) trees and phenetic (trait-based similarity) trees. It was introduced by Saitou and Nei in 1987 and relies on a distance matrix to iteratively determine which taxa (or sequences) are closest neighbors—i.e., children of the same internal parent node—until a complete tree is formed.

The NJ algorithm follows a bottom-up clustering approach, progressively merging closely related sequences (or taxa) based on their pairwise evolutionary distances. Unlike UPGMA (Unweighted Pair Group Method with Arithmetic Mean), which assumes a constant rate of evolution and considers only absolute distances, NJ accounts for variations in evolutionary rates, reducing the risk of errors.

A Neighbor-Joining tree aims to minimize the total branch length, making it a type of minimum evolution method. In addition to phylogenetic tree construction, NJ plays a crucial role in progressive multiple sequence alignment (MSA) methods, such as ClustalW, by guiding the sequence alignment process based on evolutionary relationships.

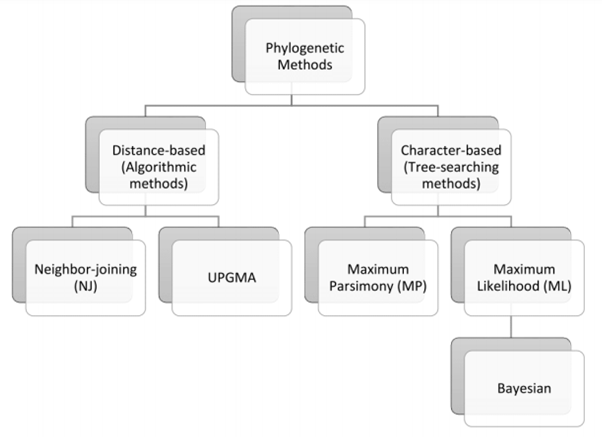
Figure 1:Phylogenetic methods used for constructing guide trees. Adapted from:

http://web.cs.elte.hu/blobs/diplomamunkak/bsc_alkmat/2015/biro_regina_krisztina.pdf

 

 

 

 

 

 

 

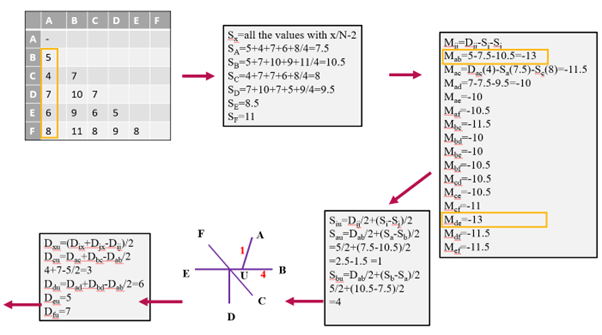
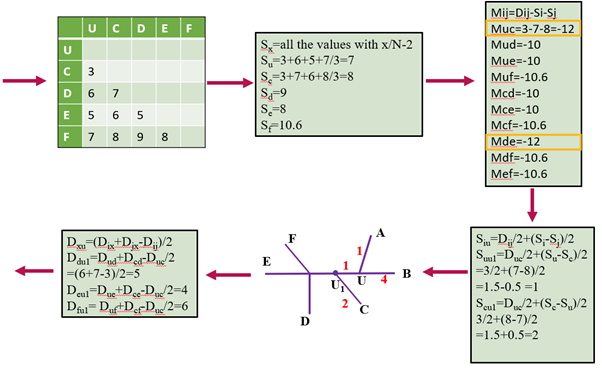
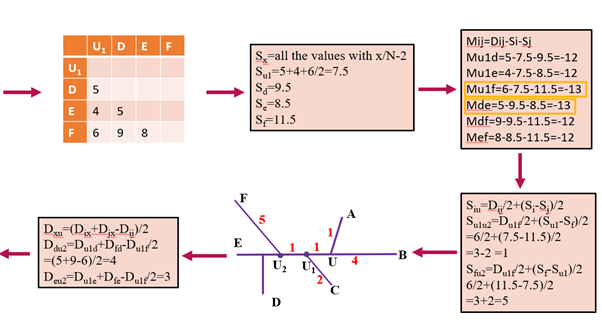
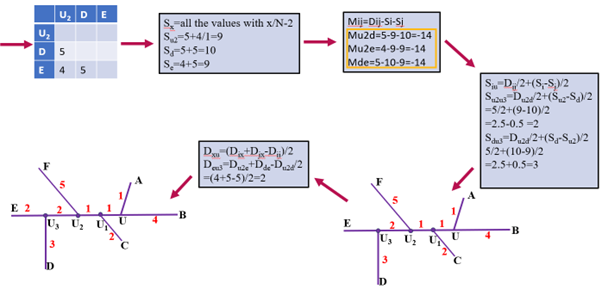
Figure 2: Example being calculated iteratively. Each color represents a step towards generating a phylogenetic tree

 

 

Advantages and Limitations

Advantages:

1. Fast and efficient for large datasets.

2. Does not require an initial tree assumption.

3. Works well with large evolutionary distances.

 

Limitations:

1. Relies on accurate distance estimation.

2. Can be sensitive to errors in distance calculations.

3. Does not account for site-specific variations in evolution.